To effectively design a river crossing, such as a culvert crossing, both the expected flood flow (design peak discharge) and the capacity for the stream crossing to pass the designed flood flow (see section 8.9.2), need to be known.
Flood flow is typically expressed in cubic metres of water per second (cumecs), for a given return period or annual exceedance probability (AEP). To calculate an AEP, divide 1 by the return period and multiply by 100. For example, a 1-in-20-year return period is equivalent to a (1/20) * 100 = 5% AEP.
The NES-PF regulations provide specific requirements for determining flood flows. It is essential that these are understood. However, prediction of flood frequency is not an exact science, and the selection of a design value for any particular site should be made carefully. For larger or more complex catchments, this should be done by an experienced hydrologist or forest engineer. The assessment should consider a range of factors including the characteristics of the catchment, the appropriateness of the model for the site being evaluated, and any local knowledge that can be obtained on historical flood events at the site.
Most forest river crossings are small and drain catchments that are unlikely to have recorded flow data. The flood frequency, flow rates and water levels of these small catchments are significantly influenced by the immediate catchment characteristics, and the stream profile. Where flood flow characteristics are not known, an estimate must be made. To do this, ideally two or more methods should be used, where available. Such methods include using historical stream flow data for a region (the regional method – see section 8.9.1), or rainfall data, together with catchment and river characteristics (the empirical method – see section 8.9.2).
It is also good forest engineering practice to verify flood estimates. This can be done by inspecting existing culverts and bridges on the same waterway, or on one similar to the proposed crossing site, to gain an indication of the approximate flood flow for known storm events. However, be cautious using this approach on large structures, as a rare flood flow, such as a 1-in-50 or 1-in-100-year event, may not have occurred since its installation. Statistically, there is only a 60% chance of experiencing a 1-in-50-year flood in any 50-year period.
8.9.1 Calculating flood flow using the regional method
Screen view of the NIWA online flood flow estimation model
Regional methods draw from New Zealand’s network of long-term river gauging stations, by fitting the observed flood records to an extreme value distribution, then extrapolating them to a catchment for which no records exist. It predicts the mean annual flood (MAF) flow in a stream or river reach, then applies a regional multiplier to estimate 1-in-10, 20, 50 and 100-year flood events.
Regional methods are well suited to rivers draining catchments larger than 1000 hectares (10 km2), and can be used with moderate confidence down to catchments of around 500 ha. These are often classed as third order streams.
The most current New Zealand regional method has been developed by NIWA. It uses the observed mean annual flood (MAF) statistics for 630 of the most reliable flow measuring sites in New Zealand, and is underpinned by 1:250,000 scale soil mapping (QMap) from GNS (Henderson and Collins, 2018). It is supported by twice as many sites, and three times the annual maxima than the previously available regional method (McKercher and Pearson, 1989). It also captures more extreme events. For example, the current version accounts for the markedly different rainfall runoff response associated with deep porous volcanic ashfall (pumice) soils in the central North Island.
The Henderson and Collins (2018) version is available through NIWA’s 2019 online flood frequency tool. See www.niwa.co.nz/natural-hazards/hazards/floods; click on ‘Go to the Flood Frequency Tool’. It allows the user to obtain an estimate for a range of flood flows of most rivers and streams in New Zealand. The NIWA online tool does not use the river network from the LINZ Topographic Map series, but rather uses its own digital terrain model (DTM) that supports their River Environment Classification (REC, Version 1). The REC DTM differs in the way it fits the modelled river network to the terrain, compared to the river location on the LINZ Topo Map series. In the example below, the fitted REC is represented by the purple lines, and the blue line is from LINZ Topo Map. REC does not model some small headwater streams.
The flow gauging stations are denoted on the map as red dots, and may be interrogated by clicking on that dot. In the ‘pop-up’ box, H_C18…., indicates flow estimated using this regional method for the selected reach. Scrolling down in the dialogue box gives the standard error in each of the estimates. Also, clicking on the arrow on the top bar toggles to the rational method estimate, but note that the values need to be extracted and multiplied by an appropriate runoff coefficient (C). Refer to engineering or regional council texts for guidance.
If the model does not show a headwater or second order river present yet one has been identified, then it is reasonable to click on adjacent reach from a similar sized catchment to get flow estimates. Keep in mind that the modelled flow is always for the most downstream point in any given reach, so in very long narrow first or second order rivers, the contributing area, and hence the flood flow, may be substantially less at the top of the reach compared to the most downstream point.
It is recommended that this tool should only be used by those who are familiar with the assumptions and limitations in the underlying hydrological models. For example, the NIWA regional model does not include factors for vegetation, unlike the empirical methods such as TM61 and the rational method. This is because in larger catchments factors such as rainfall intensity and geology (soil porosity and depth to bedrock) were found to be more significant in explaining flood magnitudes.
8.9.2 Calculating flood flow using empirical methods
Empirical methods predict flood flows from estimates of rainfall intensity for a given duration, catchment and river channel characteristics. The most widely empirical methods used in New Zealand are the rational method and TM61 (technical method 61 (1964)). The latter is a New Zealand variant of the rational method developed by the former Ministry of Works. The rational method is considered a preferred method in catchments less than 120 hectares, as it is known to yield large (that is, very conservative) values for larger catchments. Both methods are known to provide more consistent results in more uniform terrain.
The catchment rainfall data, or an estimate of it, drives the empirical flood flow estimation methods (TM61 and rational method). Rainfall data can be sourced from the NIWA high intensity rainfall data system (HIRDS). Version 4 takes account of predicted climate change. Visit hirds.niwa.co.nz. NIWA provides help and background information at www.niwa.co.nz/information-services/hirds.
TM61 requires rainfall depth and the rational method requires rainfall intensity for a given duration. These formulas provide an estimate of the design peak flow for various annual exceedance probabilities.
The HIRDS coverage of derived rainfall depths for different durations and return periods can be download for use in ArcGIS from NIWA. Each surface contains rainfall depth in mm for a given average recurrence interval in years and event duration in hours on a 2 km grid. High intensity rainfall data is also available in the format of ‘depth-duration frequency’ and ‘intensity-duration frequency’.
Rational method
The rational method is the most commonly used empirical method and its origin dates back over 100 years. It appeals because of its simplicity. Assumptions on which the rational method is based include that rainfall is uniformly distributed over the catchment (which may not hold true in larger basins), that the catchment is impervious (with the effect of detention, depression and channel storage considered negligible), and that the whole catchment contributes to runoff. These are reasonable assumptions for small basins, especially when saturated from previous rainfall events. It is appropriate to use the rational method in small catchments (up to 120 ha).
The formula is most commonly written as Q = CiA/362, where:
Q = peak discharge at design recurrence interval (m3/s)
C = rational runoff coefficient (dimensionless)
i = rainfall intensity (mm/hr) – for a calculated time of concentration (ToC) in minutes
A = catchment area (ha).
Rational method values of “C”
Source: Keller and Sherar (2003)The runoff coefficient C is a simple ratio between the depth of rain input and river outflow that occurs over various surface types when rainfall duration. The larger the C value used, the greater the modelled runoff. Chapter 5 of Keller and Sherar (2003) Hydrology for Drainage Crossing Design demonstrates how to use the rational method. While the original C factors ranged from 0.15-0.4 for forested catchments, the adjacent table represents the values to be used in what is referred to as the modified rational method, and is expected to yield better estimates as it takes into account soil types.
If an entire catchment is to be clear felled over two or three years, in most situations larger flood peaks can be expected so it is prudent to pick a higher C value. This is because there will be less interception of rainfall by vegetation. For example, in a small catchment that is completely clear-felled it is appropriate to use C = 1.0 in most situations. However, in porous soils the factor may not be as much.
The NIWA online flood estimation tool implements the rational method using HIRDs version 4, but only returns the ‘iA’ part of the equation. This leaves the user to specify C value, noting that the default value is C = 1.0.
Technical memorandum No. 61 (TM61)
TM61 was developed for New Zealand conditions in 1953 by the former Ministry of Works for use in smaller catchments; see A method for estimating design peak discharge, (MWD 1980) (http://docs.niwa.co.nz/library/public/TM61_1980.pdf). TM61 typically relies on the use of nomograms or lookup graphs. This is because it was produced prior to computer technology, but spreadsheets that have converted these graphs to equations are also available. In order to use TM61, the following information is needed:
- Catchment area
- Channel length
- Average channel slope
- Direct length (straight line distance from the culvert location to the most distant point in the catchment)
- Rainfall depth for the design storm event. For example, 20, 50, or 100-year event having a duration equal to the catchment time of concentration
- General information about catchment soil types, topography, and land cover (in small catchments it is best practice to design for worst case. That is, 100% clearfell.
TM61 requires selection of the appropriate infiltration coefficient’ (Wic), time of concentration (ToC) for the catchment and an estimate of average channel slope. The Environment Bay of Plenty (EBOP 2012) document Hydrological and Hydraulic Guidelines (www.boprc.govt.nz/media/373948/hydrological-and-hydraulic-guidelines.pdf) is a good reference and gives values of Wic for various soil types. This is particularly important for pumice because it has very different infiltration characteristics to impervious or saturated soils. Time of concentration (ToC) for a catchment is approximately the time required for runoff to travel from the most distant point in the catchment to the river crossing location. For very small watersheds, such as a few hectares, Keller and Sherar (2003) recommend selecting a minimum ToC of five minutes.
The different methods for estimating a flood flow yield can lead to different flow results. This is because their estimates are based on differing factors. For example, TM61 is expected to overestimate flow on porous volcanic soils, and to become less accurate on catchments larger than 1000 ha (Laurenson, Burton & Henderson, (1967). A University of Canterbury dissertation project (Costley, 2019) usefully demonstrates the variation in the three methods for 10 small catchments ranging from 33-700 ha. (See diagram below).
The Environment Bay of Plenty (EBOP) document stresses that professional judgement is needed when choosing an appropriate runoff coefficient, C and time of concentration.
All methods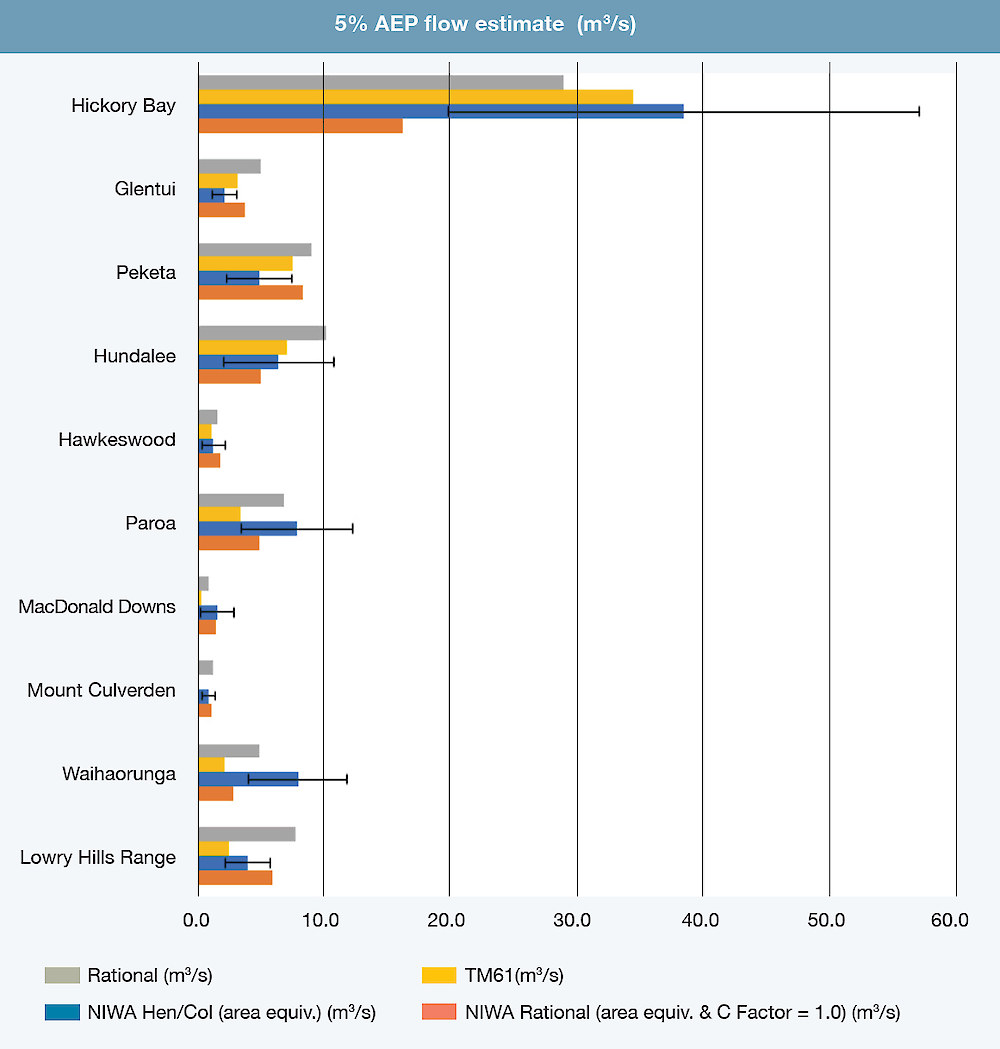
Flood estimates using Henderson and Collins (2018) regional method (the error bars indicate the standard error), TM61 and the rational method, where the runoff coefficient C was set to 1.0 to model a clear-felled catchment. (Analysis by Costley, 2019)
8.9.3 Calculating culvert size
Carefully consider a range of factors to determine the design. Larger and more complex catchments may require specialised expertise.Having derived a flood flow estimate for a design peak flow (AEP), the next step is to work out a suitable culvert size.
The flow rate of water a culvert can pass depends on many factors, including not only the size of the opening, but also the length, the slope it is installed at, the material from which it is made, and the pressure that the water is under if it is allowed to ‘head up’. Heading up refers to the water level being above the top of the culvert; this helps push the water through.
For forestry applications, a simplified chart (pages 84-86 of Keller and Sherar (2003)) is presented below that provides for a good culvert diameter estimate based only on:
- Culvert type (Headwall and Wingwalls = Type 1, Mitered = Type 2, Projecting beyond the embankment = Type 3)
- Heading up ratio (He/D). He is the depth of water; D is the diameter of the pipe. For culverts that are designed using the NES-PF permitted category, the culvert is not allowed to head up and a He/D ratio of 1 should be chosen
- He/D scales. To use Scales 2 or 3, project horizontally to Scale 1, then use a straight inclined line through Scales D (culvert diameter in meters) and Q (flow rate in cumecs).
Example
How to conservatively estimate the correct size of a corrugated metal pipe culvert, with an inlet ‘projecting beyond the embankment’, in a stream with a peak flood flow in the range of 2 and 3.5 m3/s, and where the design does not allow heading up
Use the nomogram below. Note that the lookup chart is only for corrugated culverts. A ‘projecting beyond embankment’ is a Type 3 shown at the bottom right of the chart. No heading up equates to a He/D ratio of 1.0, which is on the far-right axis. For a 2 m3/s flow event, the required corrugated metal pipe culvert diameter is between 1.2 and 1.3 m, that is, follow the dotted lower red. For a 3.5 m3/s flood flow event, the required pipe diameter is at least 1.6 m.
Headwater depth and capacity for corrugated metal pipe culverts with inlet control (metric system)
Adapted from FHWA, HDS 5, 1998
Headwater depth and capacity for concrete pipe culverts with inlet control
Adapted from FHWA, HDS 5, 1998
8.9.4 Acceptable risk of a given flood exceeding the river crossing design parameters
Choose the right type of culvert when calculating culvert size in the nomogram.A risk-based approach is normally used in the design of river crossings. In steep hill country, it is generally not practicable to design a culvert crossing to cope with the maximum creditable flood or debris flow that an exceptional storm may generate. Bridges and culvert sizes must instead be designed to meet or exceed the standards specified in the NES-PF. Generally, a minimum 50-year design life will be adopted. A forest owner will typically accept a greater risk of a crossing failure on a spur road than on an arterial road.
The table below indicates the chance of failure in a flood of a given recurrence interval. Note that this does not imply catastrophic failure, but rather the chance of a culvert not being able to pass a flood without overtopping, and the road fill sustaining some scour. For bridges there is a chance of abutments being scoured or the bridge superstructure being damaged by woody debris carried in the flood flow. The designer should also consider the consequences of a partial or complete blockage of a culvert by tree fall or logging slash. The likelihood of failure in forested catchments, especially after harvest, may be greater than that shown in the table because of additional factors like blockage or damage by woody debris.
Example
Flood recurrence interval (years) in relation to design life and probability of failure*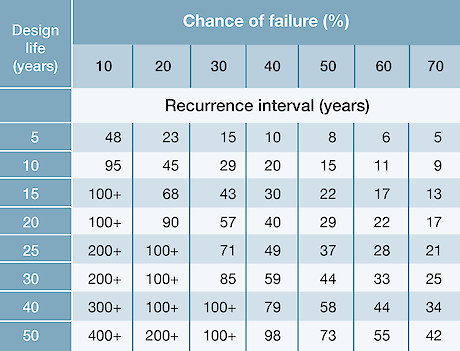
Based on formula P = 1-(1-1/T)n, where n = design life (years), T = peak flow recurrence interval (years), P = chance of P = chance of failure (%). (Source: Megahan, 1977)Using the table adjacent, if a road culvert is expected to last at least 25 years and the forest owner will accept no more than a 40% chance of failure during the road’s design life, then a 50-year recurrence interval flood event should be used in the design for sizing that culvert. The table shows it as a 49-year event, which is close enough given all the other uncertainty in the design. Refer to this link.